Gráficos 3D
Pulsa aquí para bajarte los programas de demostración
Todos hemos tenido alguna vez contacto con los gráficos vectoriales en tres dimensiones; basta con ver casi cualquier anuncio de televisión para encontrarse con lámparas y mesas que se mueven solas, coches que se transforman en tigres, gallinas bailando claque, etc. También en juegos de ordenador encontramos sofisticados gráficos en tres dimensiones, animados en tiempo real, que seguro que a más de uno ha dejado realmente sorprendido. Sin embargo, pocos son los que saben como conseguir esa maravilla de secuencias animadas, debido a la dificultad de encontrar información práctica sobre el tema. Así, he decidido escribir el siguiente artículo, el cual no pretende ser tampoco un curso intensivo (no soy ningún experto en el tema), pero sí puede servir como iniciación para entender la teoría y la práctica de este amplio campo. Así mismo, quiero explicar también los errores que cometí yo mismo al empezar, para evitar que alguien los repita y pierda el tiempo innecesariamente depurando un programa.
Uso y adaptación de los programas
Acompañando a este artículo van una serie de programas que permiten ejemplificar lo dicho en cada parte. Estos programas los he escrito en BASIC para facilitar su traducción a diversos modelos de ordenadores, así como para que todos puedan estudiarlos y entenderlos. Escribirlos en otro lenguaje más potente, como C, supondría excluir a muchos que también pueden estar interesados. Asimismo, he incluido gran cantidad de líneas REM en ellos para explicar cualquier cosa que pueda no estar suficientemente clara.
En el disco vienen preparados para funcionar con el editor QBASIC de MICROSOFT. He procurado escribir de manera estructurada para que resulten fáciles de entender y traducir para otros tipos de BASICs. Para usarlos se requiere una tarjeta gráfica compatible con CGA, MCGA, EGA, VGA, AT&T o HERCULES, si bien algunos programas no podrán ser usados con esta última debido a que necesitan 4 colores simultáneos como mínimo. Es necesario indicar al principio del programa (en el propio listado) el modo de pantalla que se desea para ejecutarlo. De esta manera se consigue un mejor aprovechamiento de las capacidades gráficas de cada ordenador. Para más información, estudiar el listado KERNEL.BAS que contiene las rutinas básicas de salida y de configuración de la tarjeta.
Para aquellos que no tengan el QBASIC, pueden conseguirlo en cualquier ordenador equipado con la versión 5.0 o superior del MS-DOS, copiando los ficheros QBASIC.EXE, QBASIC.INI y QBASIC.HLP. Los usuarios de tarjeta HERCULES deben copiar además la controladora MSHERC.COM, y ejecutarla antes de cargar el QBASIC. También se puede usar el compilador QUICKBASIC, aunque las versiones antiguas (que, por cierto, ¡son más rápidas que las más recientes!) es posible que solo acepten los modos de CGA y EGA. Yo tengo la versión 2.01 y son las únicas tarjetas que funcionan.
Si los programas van demasiado rápidos, podéis enlentecerlos disminuyendo las variables de incremento (vienen definidas al principio del programa).
Lista de los programas
Los programas marcados con un asterisco necesitan un mínimo de cuatro colores simultáneos en pantalla, por lo que no funcionarán con tarjetas HERCULES.
- KERNEL.BAS Contiene las rutinas básicas de salida para conseguir total compatibilidad con todas las tarjetas gráficas.
- PRG1.BAS Desplazamiento de un cubo en representación alámbrica.
- PRG2.BAS Uso de la base de datos optimizada.
- PRG3.BAS Rotación de un cubo en representación alámbrica.
- PRG4.BAS Efectos de la combinación de rotaciones y traslaciones.
- PRG5.BAS Rotación de un cubo con eliminación de superficies ocultas (método del vector normal).
- PRG6.BAS Rotación de dos tetraedros con eliminación de superficies ocultas (método del vector normal).
- FILL.BAS * Rutina de rellenado de polígonos cerrados.
- PRG7.BAS * Rotación de un cubo con eliminación de superficies ocultas (algoritmo del pintor).
- RELLENA.BAS Rutina de rellenado (segundo algoritmo).
- PRG8.BAS Rotación de un cubo con eliminación de superficies ocultas (algoritmo del pintor, segundo algoritmo de rellenado).
- FILL2.BAS * Rutina de rellenado con tramas.
- PRG9.BAS * Rotación de un cubo con sombreado por una fuente de luz.
- PRG10.BAS Rotación de un cubo con sombreado por una fuente de luz (segundo algoritmo de rellenado).
- CILINDRO.BAS Programa generador del prisma / cilindro.
- PRG11.BAS Rotación de un cilindro con eliminación de superficies (método del vector normal).
- PRG12.BAS Rotación de un cilindro con sombreado.
- CONO.BAS Programa generador de la pirámide / cono.
- PRG13.BAS Rotación de un cono con eliminación de superficies ocultas (método del vector normal).
- ESFERA.BAS Programa generador de la esfera / elipsoide.
- PRG14.BAS Rotación de una esfera con eliminación de superficies ocultas (método del vector normal).
- PRG15.BAS Rotación de una esfera con sombreado.
- REVOLU.BAS Programa generador de superficies de revolución no regulares.
- PRG16.BAS Rotación de una copa con sombreado (demostración de la rutina anterior).
- REVOLU2.BAS Programa generador de superficies de revolución no regulares mejorado.
- PRG17.BAS Rotación de una jarra con sombreado (demostración de la rutina anterior).
Los gráficos por ordenador: un poco de teoría
Los gráficos por ordenador surgieron a principios de los cincuenta en el famoso MIT (Instituto Tecnológico de Masachussets). En él se conectó un osciloscopio a uno de sus ordenadores, de modo que éste podía controlar directamente la posición del haz catódico. Este sistema podía realizar dibujos simples, moviendo el haz de manera que fuese trazando las líneas que lo componían. Sin embargo, cuando la complejidad del gráfico aumentaba, aparecía un problema de difícil solución: el parpadeo. Este surgía porque el punto trazado por el haz desaparecía unas décimas de segundo después de que el haz se hubiese movido, lo que obligaba a redibujar constantemente el gráfico (a este proceso se le denomina refresco). Con figuras de pocas líneas, el dibujo podía ser refrescado a una velocidad suficiente como para que no hubiese problemas, pero al aumentar el número de segmentos, el ordenador tardaba más en generar cada imagen, de modo que cuando empezaba a redibujar una línea, la original ya se había borrado totalmente. A este problema había que añadirle que el ordenador tenía que dedicar la totalidad de su tiempo de ejecución a mantener el refresco de la imagen, lo que impedía la realización de cálculos simultáneos. Posteriormente se ideó un tipo de pantalla que mantenía la luminosidad de un punto incluso después de que el haz dejase de iluminarlo, usando una especie de condensador entre el fósforo y el tubo. Para borrar la pantalla, simplemente se descargaba ese condensador. Este sistema tenía la ventaja de que eliminaba totalmente el refresco de la imagen, pues ésta se mantenía aunque el haz dejase de pasar. Sin embargo, tenía el problema de que no se podía borrar una parte de la pantalla, sino que se debía borrar toda y reescribir la parte común. A esto hay que unir el bajo contraste de la imagen.
Este sistema de generación de imágenes es denominado VECTORIAL pues sus imágenes están compuestas por vectores unidos entre sí. Pronto se hizo evidente que este sistema no era excesivamente práctico, así que se empezó a trabajar en uno más perfeccionado. El resultado fue el sistema RASTER SCAN. En él, no es la CPU la que controla el tubo catódico, sino que existe una circuitería independiente que realiza todo el trabajo. Esta vez, el haz no crea la imagen a partir de segmentos o vectores, sino que lo hace a partir de puntos (los famosos PIXELS). Para ello, el haz recorre toda la pantalla en líneas horizontales, de izquierda a derecha y de arriba a abajo. Este movimiento se realiza con el haz a baja intensidad. Si necesita activar un pixel, aumenta la intensidad en el momento en que pase encima de él. Dado que el haz tiene que recorrer siempre toda la pantalla, el parpadeo de la imagen solo dependerá de la velocidad del rayo, nunca de la complejidad de la imagen. Así mismo, al ser una circuitería externa a la CPU la que genera la imagen y la refresca, ésta queda totalmente liberada de esta tarea, pudiendo mantener una imagen en pantalla mientras realiza otros cálculos. A todo esto hay que unir la posibilidad de conseguir una amplia gama de tonos y colores, frente a la gran limitación de los sistemas VECTORIALES en este aspecto. La supremacía de los sistemas RASTER queda demostrada al comprobar que todos los ordenadores actuales lo usan, sin importar su tamaño y potencia.
La circuitería para la generación de la imagen puede estar diseñada de muy diversas formas, de modo que acepte más o menos resolución o colores. Sin embargo, en todas ellas, la imagen es almacenada en una memoria RAM especial, línea a línea, de modo que, para transferirla a la pantalla solo haya que leerla secuencialmente y transmitir los datos leídos al haz.
Hay dos posibilidades básicas para la escritura en esa memoria de video: en el más sofisticado, la placa incorpora un microprocesador propio, y acepta ordenes de alto nivel desde la CPU, como trazar rectas, círculos, mover SPRITES automáticamente, actualizar la paleta de colores, etc. De este modo, la CPU se comunica a través de puertos. Este es el caso de los MSX2, que llevan un chip específico denominado VDP (Video Display Procesor), o de la consola SUPER NES, capaz de realizar automáticamente rotaciones en 3D de una imagen, y multitud de efectos. La altísima calidad de imagen de estas máquinas demuestra la gran capacidad de este sistema. Aparte de esto, tiene la gran ventaja de descargar casi por completo a la CPU principal del trabajo de la gestión de la pantalla. A esto se le añade que la cantidad de memoria asignada a la pantalla puede ser superior a la que es capaz de direccionar directamente el microprocesador principal, sin que surjan problemas de velocidad o de transferencia de información por necesitar usar técnicas de paginación de memoria.
El otro método consiste en una circuitería que simplemente lee la imagen de la memoria de video y la plasma en pantalla. La diferencia con el otro es que la CPU accede directamente a esa memoria y escribe en ella los datos necesarios. Esto significa que tiene que estar situada dentro del espacio direccionable por la CPU, como una parte más de la memoria principal. Tiene la ventaja de que es un sistema mucho más barato y simple que el anterior, y es perfectamente válido, pues es la circuitería extra la que mantiene el refresco; sin embargo, es la CPU la que tiene que hacer los cálculos matemáticos para trazar rectas, círculos, etc. Sin embargo, estos inconvenientes se convierten en ventajas en cuanto se comprende que, de este modo, se dispone de un control total sobre la imagen presentada, pudiendo realizar sobre ésta todas las modificaciones que se deseen sin ninguna clase de limitación. Este sistema, por tanto, se usa por razones de bajo precio (el caso del Sinclair SPECTRUM, o del Amstrad CPC) o bien por la necesidad de altas prestaciones en pantalla.
Coordenadas universales, coordenadas visuales, y coordenadas específicas
Vamos primero a ver un par de conceptos muy importantes, como son los de coordenadas universales, visuales y especificas.
A la hora de trabajar con un ordenador, uno se da cuenta de la gran diversidad de dispositivos de salida que hay. Así, existen monitores, impresoras, plotters, etc, cada uno con sus propias características y capacidades. Por si fuera poco, nos encontramos con que también existen diferencias entre ellos mismos; así, nos encontramos con tarjetas gráficas CGA, EGA, con impresoras de 9 o 24 agujas, plotters con 200 o 400 puntos por pulgada, etc. Todo esto hace que, en principio, el software tenga que estar adaptado a las resoluciones de cada uno. Esto es debido a que trabajamos con las COORDENADAS ESPECIFICAS del aparato. Por ejemplo, si trabajamos con CGA, las coordenadas tendrán que darse referidas a un origen situado en la esquina superior izquierda, y con unas dimensiones máximas de 320 x 200 puntos. Si corriesemos ese programa con una EGA en el modo 640 x 350 puntos, el dibujo saldría más pequeño, pues el programa piensa que tiene simplemente 320 x 200. Además, al ser distinta la relación entre coordenadas X e Y, las figuras saldrían deformadas, achatadas.
El problema se resuelve usando un sistema de COORDENADAS UNIVERSALES y VISUALES, de modo que el programa trabaja siempre en un modo fijo, y luego estas coordenadas son traducidas a las específicas del dispositivo justo antes de ser enviadas. Vamos allá.
Las coordenadas universales se usan para definir cada uno de los objetos en la base de datos. Cada uno se define con el origen de coordenadas en su centro. No existe un límite máximo en ningún eje, sino que los objetos pueden ser tan grandes como necesitemos.
A continuación se realiza la conversión a coordenadas visuales. En ellas, el origen se encuentra, bien en el ojo del observador, bien en el centro del dispositivo de representación. Aquí lo que se hace es modificar las coordenadas de cada objeto mediante formulas de rotación y traslación para situarlos en el sitio y en la posición del espacio que le corresponde a cada uno. Al igual que antes, no existe límite en el valor de estas coordenadas. No olvidemos que trabajamos con todo el espacio.
Por último, llega el momento de convertir las coordenadas visuales en coordenadas específicas. Para ello, necesitaremos tomar un par de dimensiones proporcionales al dispositivo. Para hacer esto, hay que tener en cuenta la relación de aspecto. Veámoslo con detalle:
Cuando trabajamos con cualquier ordenador, la relación de dimensiones X e Y del tubo catódico es la misma, 3/4 (igual que los televisores normales). Esto hay que tenerlo en cuenta a la hora de definir la relación de coordenadas universales. En los programas he escogido los valores 640 x 480 porque su relación es 3/4 (igual que la pantalla) y porque son las coordenadas máximas de las tarjetas VGA en el modo de alta resolución. Esto no significa que las coordenadas visuales no puedan tener valores mayores de 640 en X y 480 en Y, sino que las coordenadas que sobrepasen esos valores saldrán fuera de la pantalla real. Desde luego, podría haber tomado 400 x 300, 4 x 3, 100 x 75, etc, que mantienen la misma relación, pero tendría que redefinir la base de datos del objeto, pues ésta supone que la coordenada máxima en X de un punto para que caiga dentro de la pantalla debe ser 640, mientras que si uso 400 x 300, esa coordenada máxima sería 400. Si usase un plotter que trabaja con hojas DIN A4, su relación de aspecto será de 210 / 290, o sea,21/29 (una hoja DIN A4 mide 210mm de ancho y 290mm de alto) ,entonces debería usar los valores 663 x 480.
Si vamos a usar simultáneamente varios dispositivos de salida con relaciones de aspecto distintas, tendremos que usar valores de relación distintos. Para calcular las coordenadas, debemos suponer primero un valor máximo de coordenadas. Ese valor indicará cual será la coordenada máxima (referida a las coordenadas visuales) que corresponderá al límite de la pantalla. En otras palabras, vamos a definir una pantalla virtual cuyas coordenadas tengan la misma relación que las dimensiones del dispositivo de salida. En mi caso, escogí 480. A continuación, hay tres posibilidades:
- relación de aspecto menor que 1: multiplicaremos el valor máximo (el que escogimos antes) por el inverso de la relación de aspecto. El valor obtenido será la dimensión en el eje X, y el valor tomado inicialmente será la dimensión en el eje Y.
- relación de aspecto mayor que 1: multiplicaremos el valor máximo por la relación de aspecto. El valor obtenido será la dimensión en el eje Y, y el valor tomado inicialmente será la dimensión en el eje X.
- relación de aspecto igual a 1: ambas dimensiones serán iguales al valor máximo.
La razón de que hagamos esta distinción es debida a que, de este modo, la pantalla virtual tendrá siempre en una de las dos coordenadas el tamaño escogido, y en la otra será siempre mayor.
Los valores de dimensión en X e Y son los que tendremos que usar en las ecuaciones de proyección como dx y dy. Esto viene explicado en el siguiente apartado.
Ahora ya tenemos hallados los valores provisionales de relación X e Y, pero, así por las buenas no nos resuelven nada. Necesitamos hallar una relación entre estas coordenadas teóricas y las auténticas del dispositivo de salida. Para ello calcularemos dos variables, RELX y RELY, simplemente dividiendo la coordenada máxima en X del dispositivo por la dimensión X, y la coordenada máxima en Y por la dimensión Y. Ahora, cada vez que queramos dibujar un punto, debemos multiplicar sus coordenadas X e Y por los valores de RELX y RELY. De este modo realizaremos el paso de coordenadas visuales a coordenadas específicas.
Proyección de puntos en cónico
Lo primero que necesitamos para realizar gráficos 3D es saber proyectar puntos tridimensionales (los del gráfico) sobre un plano (la pantalla o monitor). Para ello vamos a usar unas relaciones muy simples entre triángulos equivalentes. Vamos allá.
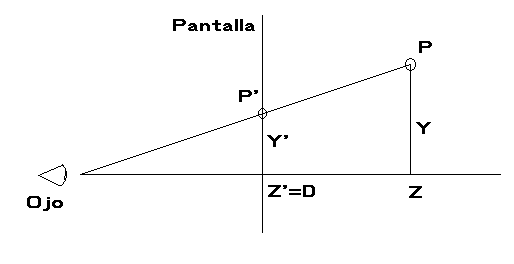
En el gráfico de arriba vemos representada la proyección del punto P, de coordenadas Y y Z (la X sería perpendicular al gráfico, así que no la representamos). El punto O es donde está situado el ojo del observador, y la línea vertical del medio es la pantalla. El punto, por tanto, se encontraría en el interior del monitor. Vemos que, al unir O con P, la línea corta a la pantalla en el punto P', que será la proyección de P sobre la pantalla.
Vemos que tenemos unas coordenadas Z, Z', Y e Y', y dos triángulos equivalentes. Z' es la distancia del observador a la pantalla, así que la llamaremos D. De este modo, para hallar la coordenada Y', que sería la coordenada Y de la pantalla, bastará que usemos un poco de trigonometría, y tendremos que:
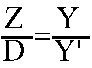
Luego, tenemos que
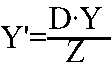
Lo mismo que decimos para la Y se debe aplicar para la X.
Esta ecuación tiene dos problemas que pueden dar algún dolor de cabeza a más de uno (a mí me los dieron): el primero, muy fácil de eliminar, es que la ecuación de arriba presupone que la coordenada (0,0) se halla en la mitad de la pantalla, cosa que no suele ser así; por tanto, si dx es la dimensión de la pantalla en horizontal (en pixels) y dy la correspondiente para la vertical, tenemos:

Debo advertir que los valores dx y dy se refieren a las dimensiones X e Y de la pantalla virtual que calculamos cuando vimos lo de la relación de aspecto del dispositivo de salida.
El segundo problema es el que más quebraderos me dio, pues las ecuaciones anteriores suponen que el origen de coordenadas está en el ojo del observador, mientras que yo suponía (triste ironía) que el origen estaba en la pantalla. Así, cuando intentaba colocar un punto en la coordenada (X,Y,0), siempre se me paraba con un error de división por cero. Por tanto, para desplazar el origen hasta la pantalla y evitarnos errores, usaremos las ecuaciones

Además de proyectar una figura en pantalla, necesitaremos desplazarla. Para ello, basta con sumar o restar a las coordenadas originales del objeto una cantidad -dx, dy, dz- que correspondan a la longitud del desplazamiento respecto del origen de coordenadas, y luego proyectar el objeto sobre las nuevas coordenadas así obtenidas.
Para ilustrar el uso de estas ecuaciones, he escrito el programa 1 (PRG1.BAS), que dibuja un clásico cubo en 3D, el cual podremos controlar desde el teclado para desplazarlo en las tres dimensiones, y apreciar así el cambio de perspectiva. Os recomiendo que estudiéis el listado, pues en el se aprecian claramente los algoritmos usados (además, es en él donde vienen las instrucciones para mover el cubo... ;-)
La base de datos optimizada
Los que hayan estudiado el programa PRG1.BAS se habrán dado cuenta de la manera en la que he codificado las líneas de la figura. Esta resulta una forma muy intuitiva y simple, pero adolece de algunos defectos. El primero es la gran cantidad de memoria que consume, pues por cada línea es necesario almacenar siete números; por otro lado, nos fijamos que al proyectar los segmentos, recalculamos los mismos puntos varias veces. En este caso concreto, las coordenadas de cada vértice son calculadas tres veces. Si bien en este ejemplo no da muchos problemas, con figuras de más líneas el proceso puede enlentecerse demasiado; y cuando veamos otras posibilidades de manipulación como las rotaciones, la eliminación de partes ocultas o el sombreado, si seguimos usando este sistema nos encontraremos con una inmensa vaca que a duras penas se mueve.
Para evitar este problema, vamos a codificar las figuras de una manera ligeramente distinta, de modo que las coordenadas de cada vértice sean calculadas una sola vez. De este modo ganaremos en velocidad y en ahorro de memoria.
El método que vamos a seguir consiste en tener las coordenadas de todos los vértices en una tabla, de modo que para trazar los segmentos no tendremos que indicarle: "traza una línea desde la coordenada X,Y,Z hasta la coordenada X',Y',Z'", sino que especificaremos "traza una línea desde el vértice A hasta el vértice B". De esta manera, en la tabla tendremos las coordenadas de los vértices ya operados y proyectados, y solo hará falta calcularlos una vez.
Para que se entienda mejor, voy a poner un ejemplo. Sea la siguiente matriz que contiene todos los vértices de la figura: en X está la coordenada X del punto; lo mismo para Y y Z. En X' e Y' están las coordenadas anteriores ya proyectadas en la pantalla.
| Punto | X | Y | Z | X' | Y' |
| 1 | 10 | 30 | 0 | 10 | 30 |
| 2 | 30 | 10 | 0 | 30 | 10 |
| 3 | 0 | 0 | 0 | 0 | 0 |
| 4 | 10 | 10 | 10 | 9.9 | 9.9 |
| ... | ... | ... | ... | ... | ... |
| n | 20 | 50 | 100 | 18 | 45.5 |
Ahora, definiríamos una nueva matriz en la que almacenaríamos las líneas de la figura; sin embargo, en vez de almacenar, por ejemplo, las coordenadas 10, 30, 0; 30, 10, 0, almacenaríamos 1,2. Esto le diría al programa que debe trazar una línea desde el vértice 1 al 2, y como ya tenemos almacenadas las coordenadas proyectadas, nos ahorramos tener que repetir el proceso de cálculo para todas las líneas que usen los vértices 1 o 2. Solo tenemos que tomar las coordenadas X' e Y' de la matriz.
El programa PRG2.BAS es, básicamente, el mismo que el PRG1.BAS, pero incluye las coordenadas almacenadas con la estructura de la nueva base de datos optimizada. La ventaja que sacamos de usarla es que antes, el ordenador tenía que calcular 32 vértices, mientras que ahora solo calcula 9 (la diferencia es evidente, ¿no?, una relación de tiempo 16:3 =8-{} ). Te recomiendo que analices el listado para entender mejor el sistema, pues es el que usaré de ahora en adelante en todos los programas.
Rotación de figuras
Una figura que solo se pueda mover a través de los tres ejes cartesianos pierde mucho atractivo. Por eso, vamos a ver como podemos hacer para imprimirle una rotación alrededor de cualquiera de los tres ejes.
Existe una matriz de tamaño 2x2 que tiene la curiosa propiedad de que, al multiplicarla por la izquierda por una matriz 1x2 que contenga las dos coordenadas cartesianas de un punto P, nos devuelve, en otra matriz 1x2 las coordenadas que obtendríamos del mismo punto P si lo rotásemos a grados respecto al origen de coordenadas. Esa matriz es la siguiente:
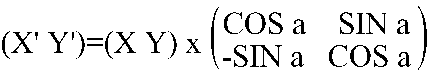
La demostración de esto vamos a suprimirla, debido a su gran extensión y complejidad. Además, seguro que casi todos se la saltarían; por tanto, dejémosla de lado y vamos a lo que nos interesa.
Alguien se habrá dado cuenta ya de que esta matriz no trabaja en tres dimensiones, sino solamente en dos, y se preguntará que podemos hacer. Bien, existen una serie de matrices, tres exactamente, de tamaño 3x3, que producen un giro alrededor de uno de los tres (va de treses) ejes coordenados. Sin embargo, no es necesario romperse la cabeza tanto, pues la matriz anterior es totalmente equivalente a esas tres (no en el sentido algebraico, sino funcional), de modo que, si queremos conseguir una rotación alrededor del eje X, le daremos a la matriz las coordenadas Y y Z; si queremos una rotación alrededor del eje Y, usaremos las X y las Z; y si la queremos alrededor del eje Z, usaremos las X y las Y. Así de fácil.
Para aquellos a los que el producto matricial no les vaya demasiado, vamos a ver como serían las ecuaciones para rotar los puntos:
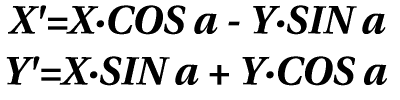
Habrá alguien que piense que puede almacenar las nuevas coordenadas en las mismas variables que las antiguas, y así se ahorra dos. La idea no es mala, pero hay que tener en cuenta un detalle: al ejecutar la primera ecuación, el valor de X cambiaría, de modo que a la segunda le llegaría un valor equivocado. El resultado sería que, al rotar las figuras, éstas se irían achatando, como plegando (puede parecer una chorrada, pero con el primer programa de rotación que hice me tiré más de cuatro horas para encontrar el fallo). De este modo, no queda más remedio que usar una variable intermedia para el nuevo valor de X. En el programa la llamo ALFA.
Como ves, rotar una figura alrededor de un eje no tiene complicación; el problema surge ahora, cuando queremos rotar un objeto sobre dos ejes simultáneamente. Entonces debemos tener mucho cuidado, pues, como todos sabemos, el producto de matrices no es conmutativo, luego no saldrá lo mismo si rotamos primero sobre el eje X y luego sobre el Y, que si lo hacemos primero sobre el Y y luego sobre el X. Esto es debido a que la segunda rotación la hacemos, no sobre el objeto original, sino sobre el objeto ya rotado.
Un ejemplo para entenderlo mejor: imaginemos un prisma recto (un cubo alargado). Si queremos hacer una animación en la que esté rotando sobre su eje, a la vez que la propia figura esté inclinada sobre otro eje, debemos calcular primero la rotación sobre el eje de la figura, y luego rotarla sobre el otro eje para inclinarla. De hacerlo al reves, veríamos el prisma inclinado, girando como si estuviese montado sobre un disco horizontal. Dicho de otra forma: si lo rotamos primero y lo inclinamos después, lo veríamos como si estuviese girando alrededor de una varilla que lo atravesase; si lo inclinamos primero y lo rotamos después, lo veríamos girar como si estuviese apoyado e inclinado sobre el plato de un tocadiscos. Dos movimientos claramente distintos. (Si no lo has entendido bien, tranquilo; más adelante hay un programa que muestra los dos movimientos).
Un detalle importante al combinar rotación con traslación: no debemos rotar una figura que esté desplazada del origen de coordenadas, sino que tenemos que rotarla primero y sumarle luego los incrementos a las nuevas coordenadas. Esto es así porque la matriz toma como eje de giro el que pasa por el origen de coordenadas. Si desplazamos el objeto primero, el eje de giro no se trasladará, de modo que lo veríamos girar alrededor de un eje paralelo al que realmente queremos; como ejemplo para explicarlo, si primero rotamos el objeto y luego lo trasladamos, rotará alrededor de sí mismo en la nueva posición, de igual forma a como rota la tierra sobre sí misma; pero si lo trasladamos primero y lo rotamos después, girará alrededor del origen de coordenadas del mismo modo que la Tierra gira alrededor del Sol.
Vamos a ver ahora la rotación alrededor de ejes que no sean los coordenados. Para conseguir esto con las ecuaciones que tenemos, lo que debemos hacer es modificar la figura mediante rotaciones intermedias para hacer que el eje de rotación deseado coincida con alguno de los tres principales, rotarla, y devolverla luego al ángulo original. Por ejemplo, si queremos rotar una figura alrededor de un eje que forma 30 grados con el eje X, 60 con el Y y 90 con el Z, no tendríamos más que rotarla 30 grados sobre el eje Z, de modo que el eje de rotación coincida con el X, rotarla alrededor de éste los grados que queramos, y volverla a rotar -30 grados sobre el eje Z para devolverla a su posición inicial.
Para ejemplificar esta parte he escrito los programas PRG3.BAS y PRG4.BAS.En el primero, podremos controlar la rotación de un cubo en tres dimensiones. El segundo muestra los efectos comentados antes al combinar rotaciones y traslaciones, así como la rotación sobre ejes distintos a los coordenados.
Aquellos que ya hallan examinado el programa 3 habrán observado que, antes de entrar en el bucle que calcula las nuevas coordenadas de cada vértice, almaceno en unas variables los valores de los senos y los cosenos de los tres ángulos. Esto lo hago así porque esos valores son constantes, y el ordenador tarda bastante en calcularlos. De este modo, ahorro tiempo de ejecución. Si piensas que es algo exagerado, te diré que, calculando los senos y cosenos con cada vértice, el programa tarda más del doble en mostrar el cubo. Y mejor no pensar si, encima, no usásemos la base de datos optimizada... Cuando veamos la generación de esferas, veremos si es necesario o no ahorrar tiempo (sobre todo si tu ordenador es lento).
Eliminación de superficies ocultas
Los ejemplos anteriores resultan poco realistas debido a un defecto de las imágenes mostradas: las partes que, en el mundo real quedarían ocultas por otras se siguen viendo. Para solucionarlo, vamos ahora a ver como borrar las partes de una figura en tres dimensiones que quedan ocultas detrás de otras.
Una característica común a todos los métodos de eliminación de superficies ocultas es el método de almacenamiento de las figuras. Estas no se almacenan como líneas, como hemos hecho hasta ahora, sino como porciones de planos. Esto es: si representamos un cubo, no almacenaremos los 12 segmentos que lo componen, sino los seis planos correspondientes a cada cara. Cada uno de estos planos sí los almacenaremos con el convenio seguido hasta ahora. Esto es: almacenamos primero todos los vértices de la figura, y luego indicamos qué vértices componen cada cara, en orden. Para que la cara esté cerrada, sería necesario indicar al final el vértice inicial, pero como suponemos que todas van a ir cerradas, podemos hacer que la propia rutina lo haga, uniendo, al final, el último vértice con el primero.
1: Método del vector normal al plano
Este método se basa en no pintar aquellas caras del objeto que miran hacia detrás de éste. Para ello, los vértices de cada plano deben escribirse en sentido antihorario. Veamos por qué:
Lo primero que necesitamos hallar es un vector perpendicular o normal al plano que define la cara que estamos tratando. Para ello, cogemos dos segmentos consecutivos, y los multiplicamos vectorialmente, tomando sus coordenadas como coordenadas de vectores. Esto nos dará las coordenadas de un vector que cumple la condición de perpendicularidad a los dos iniciales. Sin embargo, no olvidemos que el producto vectorial no es conmutativo, por lo que, para que este vector apunte hacia el exterior de la figura, es necesario que los vértices de cada plano estén definidos en sentido antihorario.
Por lo tanto, para definir cada plano, debemos imaginarnos la figura de tal modo que el plano que vamos a traducir a datos esté mirando hacia nosotros, y escribir entonces las coordenadas de los vértices en sentido antihorario.
Una vez que tenemos las coordenadas de esos vectores normales al plano, llega el momento de aplicar el test de visibilidad. Para ello, hallaremos las coordenadas del vector que une el ojo del observador con un vértice cualquiera de la cara a testear. Una vez hecho esto, aplicamos el producto escalar de este vector y el normal a la superficie, y obtendremos un valor dependiente del ángulo que forman.
Ahora es fácil. Si éste valor es uno, entonces el vector apunta hacia el observador, y si es cero, será normal al vector que une el vértice con el ojo del observador. De aquí deducimos que, si el valor resultante es positivo, la cara está mirando hacia la parte delantera del objeto, o sea, hacia nosotros, y entonces la pintaremos.
Si el valor es negativo, la cara está mirando hacia atrás del objeto, así que no la pintaremos. Si el valor es cero, la cara es normal a nosotros, luego podríamos dejarla sin pintar, pues quedaría reducida a una simple línea.
Ventajas e inconvenientes
Este método tiene la clara ventaja de su rapidez y su relativa simplicidad de aplicación, y es útil para usar con figuras no excesivamente complicadas, y cuando solo hay una en pantalla.
Entre sus inconvenientes, el primero es que no funciona bien con figuras convexas, porque en éstas, las superficies pueden quedar parcialmente cubiertas por otras, por lo que solo se vería una parte de ellas. Sin embargo, el algoritmo solo es capaz de decidir si una superficie se ve o no se ve, no si queda parcialmente oculta. De este modo, estas superficies siempre se pintarían completas, restando credibilidad a la imagen.
El otro inconveniente surge cuando se tienen varios objetos en pantalla. Entonces, aunque en cada objeto se eliminen correctamente las superficies ocultas, puede ocurrir que uno se superponga sobre otro. Cuando esto ocurre, se verán los dos, uno a través del otro, como si fuesen transparentes, aunque cada uno solo tendrá las caras visibles.
Para ejemplificar todo esto he escrito el programa PRG5.BAS, que ilustra un cubo con eliminación de superficies ocultas al que podremos rotar como queramos, y el programa PRG6.BAS, que muestra dos figuras simultáneas, para comprobar las limitaciones de este método. Te recomiendo que examines el listado para comprender bien el sistema.
2: El algoritmo del pintor
Este método se basa en una propiedad usada por los pintores de cuadros (de ahí su nombre). Si sobre una hoja pintamos un paisaje, y, una vez terminado, pintamos una persona, la pintura que usamos para dibujarla tapa perfectamente las zonas del paisaje original que había en el lienzo. De igual manera, si dibujamos los distintos planos que componen la figura desde el más alejado hasta el más cercano, a la vez que los vamos coloreando, los planos recientes irán tapando a los que ya había pintados, de modo que, al final, obtendremos la figura perfectamente dibujada, sin partes de más.
Veamos la aplicación práctica. Lo primero que hay que hacer es hallar la media aritmética de los vértices de cada plano. Esto nos dará el punto medio de cada uno. Ahora calcularemos la distancia de cada uno de esos puntos medios hasta el ojo del observador. Una vez que lo hayamos hecho, cogeremos la mayor de esas distancias. El plano al que le corresponda será el más alejado y, por tanto, el primero en ser pintado.
Para colorear los planos, los lenguajes suelen incluir diversas opciones. El QBASIC también la incorpora bajo la forma de la instrucción PAINT; sin embargo, no siempre dispondremos de estas comodidades, por ejemplo si trabajamos directamente en ensamblador, por lo que hemos de simularla con una pequeña subrutina. Además, de existir, no siempre se ajustarán a nuestras necesidades, por lo que a veces será necesario reescribirlas. Eso mismo he hecho yo. Sin embargo, en los ejemplos, debido a que su velocidad es excesivamente lenta por estar escritas directamente en BASIC, sí resultaría más ventajoso usar las instrucciones incorporadas. Trabajando en otros lenguajes como C, este factor no sería de importancia. De todos modos, los programas no pretenden ser para uso comercial, sino ejemplos de como se puede hacer lo que aquí explico; por eso les he incorporado estas rutinas en vez de aprovechar las capacidades del lenguaje.
Vamos a ver dos algoritmos. El primero se basa en la figura pintada en la pantalla, y precisa conocer un punto cualquiera interno a ella. La instrucción PAINT del QBASIC trabaja de esta manera. El segundo es más perfeccionado, si bien necesita conocer los vértices de la figura.
Para usar el primer algoritmo, necesitamos conocer un punto interior a la figura. Para hallarla, bastará con usar la media aritmética de los vértices del plano a pintar. De ese modo, siempre empezará en un punto interior a éste. Sin embargo, no podemos empezar a pintarlos así como así, sino que debemos tomar ciertas precauciones. No olvidemos que, al pintar un nuevo plano, podemos estar rellenando encima de otra cara, y si el color de esa cara coincide con el del plano que estamos pintando, la rutina de fill no funcionará correctamente, pues nos dejará partes sin rellenar. Para encontrar solución, veamos como funciona la rutina de rellenado:
- comprueba si el punto de inicio tiene el mismo color con el que vamos a pintar. Si es así, termina.
- Si tiene un color distinto, píntalo del color deseado.
- Pasa al punto de la derecha.
- Si tiene un color distinto, píntalo del color deseado y vuelve al paso 3.
- Si tiene el color con el que pintamos, vuelve al punto de inicio.
- Pasa al punto de la izquierda.
- Si tiene un color distinto, píntalo del color deseado y vuelve al paso 6.
- Si tiene el color con el que pintamos, vuelve al punto de inicio.
- Termina.
Es obvio que, si una rutina hiciese esto, solo pintaría una línea, por lo que hay que repetirlo para todos los puntos superiores e inferiores al inicial, hasta que la condición del primer paso se cumpla. Entonces la figura estará rellena. De hecho, si la figura tiene concavidades, este algoritmo puede fallar. Por eso en los programas uso uno algo más complejo, el cual describo más adelante.
Si nos fijamos, vemos que la figura a rellenar tiene que estar delimitada por líneas del color con el que estamos rellenando, y que cualquier otro color será ignorado. De este modo, si primero pintamos la cara con un color especial, que reservaremos para esta función, y luego la pintamos con el color que realmente queremos para ella, habremos eliminado el problema: si había alguna línea del mismo color que la cara actual, debida a algún plano pintado anteriormente, quedará eliminada al rellenar antes con el color especial. El único requisito es no usar ese color clave para ninguna superficie de la figura.
Este sistema es muy conocido, y puede resultar muy útil en muchas circunstancias. Una gran ventaja es que no necesita ninguna información sobre la figura a rellenar: ni vértices, ni lados. Sin embargo, tiene muchas limitaciones. La más grave es que precisa conocer un punto interior a la figura para saber donde debe empezar a rellenar. Es muy usada en programas de dibujo.
Para resolver este problema, existen otros sistemas, los cuales requieren más información sobre la figura a rellenar. A continuación voy a explicar uno de fácil aplicación, que me explicó Jesús Cea Avión:
Debemos crear primero dos tablas de igual dimensión, capaces de contener cada una tantos números enteros como pixels de alto tenga la pantalla. Serán las tablas MAX y MIN. Rellenaremos la tabla MAX con cero, y la tabla MIN con el número de pixels que tiene de ancho la pantalla (la razón de esto la veremos más adelante).
A continuación pintaremos todas las líneas de la figura, usando cualquier algoritmo de trazado. Yo he escogido el siguiente (para una línea desde X0,Y0 hasta X1,Y1):
- Hacemos DX = X1 - X0 y DY = Y1 - Y0
- Si DX > DY tomamos PASO = 1 / DX; si DY > DX tomamos PASO = 1 / DY
- Si DX = DY = 0 tomamos PASO = 1
- Hacemos un bucle N desde 0 hasta 1, con incremento de valor absoluto de PASO
- Pintamos el punto de coordenadas X = X0 + N * DX , Y = Y0 + N * DY
- Cerramos el bucle
Sin embargo, en cada paso debemos comparar el valor de X con el contenido en las tablas MAX y MIN, usando como índice el valor de Y. Si X es mayor que MAX (Y), almacenaremos X en MAX (Y). Si X es menor que MIN (Y), almacenaremos X en MIN (Y). Lo que queremos conseguir es almacenar las coordenadas X e Y de los puntos de la figura que están más a la derecha y más a la izquierda. De este modo, cuando terminemos la figura y queramos rellenarla, solo debemos hacer un bucle desde 0 hasta el valor máximo de coordenada Y de pantalla, y trazar una recta desde la coordenada X = MIN (Y) hasta X = MAX (Y). Sin embargo, si MIN (Y) es mayor que MAX (Y), significa que en esa coordenada Y no se trazó ningún punto, por lo que no debemos trazar ninguna recta (esta es la razón de inicializar las dos tablas con aquellos valores).
En realidad, el paso 5 no es necesario, pues la rutina no se basa en la imagen de pantalla para rellenar la figura. De este modo, podemos ahorrar tiempo de ejecución si no pintamos las rectas a medida que las calculamos. Así mismo, podemos anotar las coordenadas Y mínima e Y máxima, y usarlas como límites del bucle. De ese modo ahorraremos el pasar por zonas que no hay que rellenar. Esto no elimina la inicialización de las tablas antes de rellenar cada objeto, pues, en teoría, puede ocurrir que un objeto tenga alguna zona intermedia que no haya que pintar.
Este algoritmo tiene un inconveniente, a saber, que las figuras tienen que ser convexas horizontalmente; esto es, que cogiendo dos puntos cualesquiera de la figura, alineados horizontalmente, la recta que los une no debe salir fuera de ella.
Esta limitación es mayor en nuestro caso, pues nosotros rotamos las figuras, por lo que una que sea horizontalmente convexa, si la rotamos, puede dejar de serlo. Por eso, las figuras que usemos deben ser totalmente convexas (ojo, me estoy refiriendo a los polígonos que definen cada cara, no a la figura tridimensional en sí).
Ventajas e inconvenientes
La primera ventaja que tiene este método es que elimina todas las caras que no se ven, mientras que el método anterior, bajo ciertas condiciones, podía dejar caras que realmente no se verían.
La segunda ventaja es que también elimina trozos de caras parcialmente ocultas por otras, con lo que arreglamos de un plumazo el principal problema del otro sistema. Por si fuera poco, el algoritmo también funciona razonablemente bien cuando hay varias figuras en pantalla solapándose. La única precaución que hay que tomar en este caso es que, al ordenar los planos del más alejado al más cercano, no debe hacerse con los de cada objeto por separado, sino que debe hacerse con todas las caras de todos los objetos en conjunto.
Un inconveniente que tiene es que, cuando hay dos planos tocándose, la rutina puede presentar problemas para pintarlas correctamente. Es un caso algo extremo, pero puede darse.
Debido a la lentitud de algunas rutinas de FILL, se puede realizar una combinación de este método con el del vector perpendicular al plano, pues este último quita aquellas caras que, seguro, no se van a ver, dejando solo aquellas en las que hay dudas de si se ven o no. De este modo, si a las caras que deja el algoritmo del vector perpendicular le aplicamos el algoritmo del pintor, al tener que pintar menos caras, ganaremos en velocidad.
Para ejemplificar esta parte, he escrito el programa PRG7.BAS. En él, podremos rotar un cubo abierto. Debido a la lentitud de la rutina de rellenado, no me ha quedado más remedio que hacer que la figura sea rotada sin eliminar las partes ocultas y, una vez colocada en la posición deseada, pulsar R, para activar el algoritmo. Este se encuentra aislado en el programa FILL.BAS. Si usáis la versión 2.01 del QUICKBASIC, el programa irá a una velocidad razonable, incluso en ordenadores 8088 y 8086 (con CGA, eso sí). Sin embargo, con el QBASIC, la lentitud es excesiva. Lastima :-(. Debo avisar que los usuarios de tarjeta gráfica HERCULES no podrán probarlo, debido a que necesita cuatro colores simultáneos. Existen, no obstante, programas emuladores de CGA. No se que tal funcionarán, pero pueden ser una solución. Los que quieran velocidad, pueden usar la instrucción PAINT del QBASIC, colocandola en el inicio de la rutina de rellenado.
Está también el programa PRG8.BAS, que usa el segundo sistema de rellenado. Este sí puede ser usado por todos, incluso en modos monocromos. Por último, el programa RELLENA.BAS contiene la rutina aislada.
El algoritmo de rellenado inteligente
El algoritmo de rellenado presentado en el apartado anterior (el primer método) presenta algunas deficiencias. Estas son que, si hay zonas accesibles solo a través de pasadizos, o bien ciertos picos, etc, la rutina los dejaría sin pintar, debido a que es muy simple. Para evitarlo, vamos a desarrollar un nuevo algoritmo, que subsane estos problemas. Este algoritmo es, precisamente, el usado en el programa de demostración, debido a sus superiores capacidades. Su funcionamiento es, salvo algún que otro detalle, identico al de la instrucción PAINT. Tiene el inconveniente, eso sí, que, al estar escrito en BASIC, va terriblemente lento (que digo lento, LENTISIMO :'-( . Esa es la razón de que el programa no sea en tiempo real como los anteriores.
El organigrama (por llamarlo de alguna manera) de la nueva rutina es el siguiente:
- Comprueba si el punto inicial es del color con que rellenamos
- Si es así, retorna
- Pon las variables ESTADO1 y ESTADO2 a cero
- Muévete a la izquierda hasta encontrar un punto del color seleccionado
- Pinta el punto con el color seleccionado
- Si ESTADO1 es uno y el punto superior al actual es del color con el que rellenamos, pon ESTADO1 a cero
- Si ESTADO1 es cero y el punto superior al actual no es del
color con el que rellenamos:
- guarda las coordenadas del punto superior en la pila
- pon ESTADO1 a uno
- Si ESTADO2 es uno y el punto inferior al actual es del color con el que rellenamos, pon ESTADO2 a cero
- Si ESTADO2 es cero y el punto inferior al actual no es del
color con el que rellenamos:
- guarda las coordenadas del punto inferior en la pila
- pon ESTADO2 a uno
- Pasa al punto de la derecha y repite hasta encontrar un punto del color con el que estamos rellenando
- Saca las últimas coordenadas metidas en la pila
- Si el punto de esas coordenadas no es del color con el que estamos rellenando, vuelve al punto 3)
- Si el punto de esas coordenadas es del color con el que estamos rellenando y la pila no está vacía, vuelve al punto 10
- Retorna
La razón de que me desplace primero totalmente a la izquierda es que, de no hacerlo, la pila tiende a crecer de manera incontrolada, aún con figuras simples.
Además de todo esto, he incluido una pequeña protección: puede darse el caso de que, debido a errores de redondeo por parte del ordenador, la rutina de FILL empiece a rellenar fuera de la zona delimitada. Esto puede ocurrir en el caso de superficies muy pequeñas, o que están casi perpendiculares al vector de visión. En estos casos, la rutina intentaría pintar hasta el infinito.Para evitarlo, si llega a los extremos laterales de la pantalla sin encontrar un límite, dejaría de pintar esa superficie. De este modo, evitamos un 'pseudocuelgue' de la máquina. En la rutina uso la variable HEY para saber si ha ocurrido dicho error.
Este algoritmo es algo más complejo, pero funciona perfectamente, y (casi) nunca comete errores. Para poder examinarla, la he aislado en el programa FILL.BAS.
3: El método Z-BUFFER
El método del Z-BUFFER se basa en el mantenimiento de una base de datos con la coordenada Z de cada punto pintado en la pantalla. De este modo, cuando se va a pintar uno nuevo, se comprueba primero este buffer para saber si se debe colorear o no. Veámoslo con más detalle:
Lo primero que necesitamos es reservar un área de memoria capaz de almacenar tantos enteros como píxels tenga la pantalla. Si trabajamos con una resolución de 320 por 200, necesitaremos, por lo menos, 128000 bytes de reserva (usaremos dos bytes por píxel). Esta tabla debe inicializarse al máximo valor posible, esto es, todos los píxels deben tener asignada una profundidad de 65535.
A continuación, empezamos a pintar la primera cara. Para ello, almacenamos en el buffer la coordenada Z de cada punto que coloquemos en pantalla, tanto si pertenece a las líneas del contorno como si son del relleno. De este modo, tendremos en el buffer un 'dibujo' de la cara rellenada con una indicación de la profundidad de cada punto.
Empezamos con la segunda cara, pero antes de pintar cada punto, comparamos la coordenada Z de éste con el valor almacenado en el buffer de pantalla. Si es menor, lo pintamos y actualizamos el valor; si es mayor, no lo pintamos. Así con todos los puntos de los contornos y del relleno. Esto se repite para el resto de las caras.
¿Qué conseguimos con esto? Si pintamos un punto en las coordenadas X e Y de la pantalla que, en la realidad, está a 10 centímetros de esta, y luego tenemos que pintar otro punto de otra cara sobre esas mismas coordenadas, pero que está a 5 centímetros, es obvio que el píxel debe actualizarse con el nuevo color; pero si está a 15 centímetros, está detrás del primero, por lo que el píxel no debe cambiar. Por eso almacenamos la coordenada Z de cada punto presentado en pantalla, porque de este modo, sabemos si el nuevo punto a pintar está delante o detrás del antiguo. Esa es la razón, también, de que inicialicemos la tabla al máximo valor posible. De ese modo, cualquier punto que se coloque en un píxel no activado estará más cerca que el 'original'. Si la inicializásemos a cero, todos los puntos estarán a más distancia que cero, por lo que no se pintaría ninguno.
Si nos fijamos, vemos que, en el fondo, la base del sistema Z-BUFFER es identica a la del algoritmo del pintor (esto es, que las partes más cercanas se pinten sobre las más lejanas). Sin embargo, el Z-BUFFER va más allá, al tratar directamente con cada punto individual de la imagen, en vez de generalizar para toda la cara.
Ventajas e inconvenientes
La gran ventaja de este método es que es infalible. No importa lo compleja que sea la imagen, siempre dará resultados impecables. Los inconvenientes: la dificultad de programación, la gran cantidad de memoria necesaria para mantener el buffer de pantalla, y la excesiva lentitud del sistema. En grandes ordenadores el proceso suele llevar algunos minutos, mientras que en sistemas caseros, puede tardar horas e incluso días; todo depende de la complejidad de la imagen :'-(.
Para paliar en la medida de lo posible la cantidad de memoria necesaria, se ideó el método de la LINEA DE EXAMEN. Es idéntico al sistema Z-BUFFER, salvo en que, en vez de almacenar toda la pantalla, se almacena sólo una línea de píxels de cada vez, tratando únicamente los puntos cuya proyección corresponde a las coordenadas de ese scan. Repitiendo el proceso para todas las líneas de la pantalla, se consiguen resultados tan excelentes como con el sistema Z-BUFFER. Eso sí, a costa de mayor dificultad de programación y tiempo de proceso.
No he incluido ninguna demostración de estos dos sistemas debido a la gran lentitud del BASIC y su limitada cantidad de memoria disponible.
Sombreado de objetos
Vamos ahora a ver el sombreado de las caras de un objeto. Cuando tenemos una figura real, vemos que cada cara recibe una intensidad de luz distinta, según cual sea su orientación respecto a una fuente de luz. De este modo, vemos que cuando una superficie está orientada hacia una lámpara, por ejemplo, muestra la máxima claridad posible; y, a medida que se gira, se va oscureciendo, hasta quedar sin luz cuando está perpendicular a la fuente.
Para conseguir este importante efecto, vamos a aprovecharnos otra vez del producto escalar y vectorial, de igual modo que lo usamos para eliminar las superficies ocultas.
Si tenemos un foco de luz puntual, éste estará iluminando el objeto, produciendo sombras en cada una de sus caras. Si, por medio del producto vectorial, calculamos el vector normal a la cara que estamos tratando, lo convertimos en VECTOR UNITARIO, y lo multiplicamos escalarmente por el VECTOR UNITARIO que une el foco de luz con la cara, obtendremos un valor entre -1 y 1, que será proporcional al grado de iluminación de esa cara. Está claro que si el valor es negativo, esa cara está de espaldas al foco de luz, por lo que siempre estará a oscuras (en objetos cuyas caras sean visibles por ambos lados esto no es del todo cierto). Hay que hacer notar un detalle: es necesario usar los vectores unitarios en este producto escalar porque, de no hacerlo así, el valor devuelto no estará en el rango -1, 1. Además, ese intervalo no sería el mismo para todas las caras, por lo que el escalado de grises no sería uniforme para todo el objeto (o sea, caras que reciben la misma luminosidad pueden aparecer con grises diferentes).
Hay que advertir que este sistema no basta, pues hay caras que, obviamente, no vemos; por eso hay que combinarlo con algún sistema de eliminación de caras ocultas.
Si usamos el sistema del vector normal a la superficie, aprovechamos que ya tenemos calculado el vector normal a la cara que estamos tratando, y lo multiplicamos escalarmente por el vector de visión. Desde luego, los vértices de las caras tienen que estar definidos en sentido antihorario (ver SISTEMAS DE ELIMINACION DE CARAS OCULTAS).
Por tanto, para sombrear adecuadamente un objeto, debemos rellenar aquellas caras que se vean (para eso calculamos el producto escalar del vector normal y el de visión) con un color o un entramado proporcional al grado de luz que reciban (el cual obtenemos del producto escalar del vector normal y el de iluminación).
Si usamos el algoritmo del pintor, debemos tomar las mismas precauciones: pintar primero de un color clave y luego con el definitivo; desde la cara más alejada a la más cercana. Aquí, sin embargo, no hace falta que los vértices de las caras estén definidos en sentido antihorario. Sí calcularemos el producto escalar del vector de visión con el normal a la superficie. La diferencia viene ahora: si ambos productos escalares (el de visión y el de iluminación) tienen el mismo signo, significa que esa cara la vemos por el lado iluminado; por tanto, la rellenaremos con tramas. Si tienen signo distinto, la estamos viendo por el lado no iluminado. Habrá que rellenarla de negro.
Normalmente, suele haber una cierta luz difusa en el ambiente, que hace que las caras no iluminadas directamente, lo estén de un modo indirecto. Por eso, las caras que se ven pero que no están iluminadas, conviene rellenarlas con el color o trama más oscuro que haya, en vez de dejarlas en negro. Los programas permiten elegir un nivel de luz ambiental, de modo que las caras que no estén iluminadas por el foco puntual, aparezcan con una claridad correspondiente. Desde luego, a cada nivel de luminosidad de cada cara se le deberá sumar el nivel de luz ambiental, pues recibirá ambos tipos de iluminación.
Debemos tener en cuenta otro detalle: en la vida real, los objetos no suelen ser de un color uniforme, sino que presentan todo tipo de tonos en cada una de sus caras. Este es un efecto a tener en cuenta a la hora de sombrear un objeto. Para ello, el entramado a usar debe ser del color de la cara. Así conseguiremos distintas intensidades de cada color.
Por último, indicar que para hallar el vector que une la cara con el foco luminoso, da mejores resultados usar como coordenadas la media aritmética de las coordenadas de la cara; esto es así porque la media nos da el punto medio de la cara, el cual es mucho más representativo que uno de los vértices.
Para ejemplificar esta parte, he escrito el programa PRG9.BAS. En él, se sombrea un cubo como en el de el resto de las demostraciones. Debes rotar la figura como de costubre hasta situarla en la posición que quieras. Pulsa R y el programa te preguntará la colocación de la fuente de luz. Esta está siempre a la distancia de los ojos, y sólo podemos cambiar su posición en altura y en horizonte. Al igual que la demostración anterior, es MUUUUY LENTA, por culpa de la rutina de rellenado. Así que tómatelo con calma y paciencia. Por cierto: los usuarios de HERCULES no podrán usarlo, debido a que necesita cuatro colores como mínimo para trabajar. Supongo que con un emulador de CGA funcionará sin problemas.
El programa PRG10.BAS hace lo mismo, pero usando el segundo algoritmo de rellenado, por lo que podrá ser usado por todos los usuarios.
Antes de cerrar este apartado, debo decir que este sistema es muy simple, y no tan realista como otros. Esto es debido a que considera que cada cara tiene una iluminación uniforme en toda su superficie. En la realidad, por el contrario, los extremos de una cara tienen un tono distinto de la parte central, debido a que cada punto recibe la luz con un ángulo distinto. La gradación uniforme (tal y como la realizan los programas) solo sería posible si la fuente de luz estuviese en el infinito.
Existen varios algoritmos capaces de eliminar este problema. El más simple es el algoritmo de Gouraud. Se trata de tomar las intensidades correspondientes a cada uno de los vértices de la figura, y realizar un promedio de ellos para cada uno de los puntos de la figura. Yo añadiría además el punto central, para simplificar el cálculo. De este modo, el programa debe tomar triángulos formados por dos vértices consecutivos y por el punto central, y realizar en él la gradación de grises, en vez de tomar toda la cara de una sola vez. De este modo no importa el número de vértices de la figura ni su geometría, pues todo el problema se reduciría siempre a realizar el cálculo para un triángulo genérico. Además, mejora la gradación en caras casi, o totalmente perpendiculares al haz de luz.
Algoritmo de rellenado con tramas
Para conseguir la apariencia de grises en cada cara, he usado entramados de pixels. Para poder trabajar con ellas, ha sido necesario modificar la rutina de FILL original.
Lo primero que necesitamos es definir en una variable las tramas que vamos a usar. Usaremos una de tres dimensiones: en la primera, almacenaremos el número de trama que es; en la segunda, la coordenada X, y en la tercera, la coordenada Y. Al darle esos tres valores, la variable nos devolverá un uno o un cero, indicativo de si ese punto hay que ponerlo en negro o en blanco.
La rutina de FILL rellenará el área inicialmente con el color 1 para determinar las zonas a entramar, y luego las rellenará con la trama correspondiente. Veamos como lo hace:
Lo primero, hay que cambiar un poco la rutina, pues ahora no debe pararse cuando encuentre el color 1, sino cuando no lo encuentre. Para ello, donde se compare el color del punto de pantalla con el color a rellenar, si pone = se cambia a <>, y viceversa. Así mismo, se cambia el color a rellenar por 1, pues es ese el que se ha usado para delimitar el área.
Hay que hacer un segundo cambio: en la subrutina que pinta el punto actual del color deseado, debemos hacer lo siguiente:
- hallamos el resto de la división de X entre 6 (suponemos que usamos tramas de 6x4 puntos)
- hallamos el resto de la división de Y entre 4
- tomamos esos valores como coordenadas X e Y para la variable que almacena las tramas
- multiplicamos el resultado de la variable por el color con que queremos rellenar (la trama se hará con ese color y con negro; esto nos permite usar tramas de diversos colores)
- pintamos el punto actual con el color resultante de 4)
Esta rutina de rellenado está aislada en el listado FILL2.BAS para que sea fácilmente analizable.
Para adaptar el segundo algoritmo de rellenado de modo que use tramas, basta con pintar cada punto siguiendo el proceso de antes. Sin embargo, debe hacerse también con las líneas interiores, no solo con las de los bordes.
Superficies de revolución:
No siempre será necesario calcular a mano los vértices de la figura a representar y realizar su unión en líneas. En el caso de ciertos objetos, podemos encomendar la tarea a una pequeña rutina, gracias a propiedades como simetría, ejes de rotación, etc.
Este es el caso de las superficies de revolución. Estas figuras surgen de la rotación de un plano de forma determinada, alrededor de un eje. El cilindro, el cono y la esfera son los ejemplos más comunes de superficies de revolución.
Estas superficies, en teoría, tienen infinitas caras, por lo que vamos a usar una aproximación, limitándolas a un número más manejable; por ejemplo, 15 caras.
1: El prisma/cilindro
Podemos imaginar un cilindro como un prisma de infinitos lados, y cuyas bases, por tanto, son círculos. Para representar un prisma, debemos crear dos polígonos paralelos, y unir cada punto del primero con el correspondiente del segundo. Si queremos dibujar un cilindro, las bases tendrán que ser círculos. Dado que un círculo tiene infinitos puntos, nos llevaría mucho tiempo calcularlos todos :-) , así que usaremos un polígono con un número suficiente de lados como para que parezca una circunferencia.
Necesitaremos tres parámetros para definir el prisma: el radio de su base, la altura, y el número de lados que usaremos para definirlo.
Para calcular los vértices del prisma, necesitaremos echar mano de la trigonometría. Llamaremos PASO al número de lados que usaremos, y STEP a la cantidad PASO/360. Haremos un bucle B que vaya desde 0 hasta 360 - (STEP / 2) , con un incremento de STEP. Podríamos hacer que vaya hasta 360 - STEP; sin embargo, en la práctica, pueden surgir problemas de redondeo para ciertos valores de PASO, dejando alguna cara sin hacer. Si bien en el prisma o cilindro no da problemas, con la esfera sí los da, y bastante grandes. Por eso, tomando STEP / 2 nos aseguramos de que hará todas las caras.
A la coordenada X le daremos el valor RADIO * SIN (B) , a la coordenada Z el valor RADIO * COS (B) y a la coordenada Y el valor ALTURA / 2 si es la base inferior o el valor -ALTURA / 2 si es la base superior (B es la variable del bucle). Podemos hacer que una base tenga un radio distinto de la otra. Para ello, debemos usar RADIO1 * SIN (B) en X, RADIO1 * COS (B) en Z y ALTURA / 2 en Y para una de las bases, y RADIO2 * SIN (B) en X, RADIO2 * COS (B) en Z y -ALTURA / 2 en Y para la otra base.
Para unir los vértices, habrá dos pasos: unir las bases y unir las caras.
Para unir las bases, se une el vértice N con el N + 1, o el N con el N - 1 según sea la cara inferior o la superior. Esto se hace así para que cada cara quede definida en sentido antihorario, y podamos usar el método del vector normal al plano. No olvidemos que los números asignados a los vértices de una cara van de cero a PASO - 1, y los asignados a la otra van desde PASO hasta PASO * 2 - 1.
Para unir las caras, debemos hacer un bucle N desde 0 hasta PASO - 1, y uniremos:
- vértice N a vértice N + PASO
- vértice N + PASO a vértice N + PASO + 1
- vértice N + PASO +1 a vértice N + 1
Este proceso unirá las caras en sentido antihorario. No olvidemos que la rutina de dibujo cierra automáticamente las caras, pintando una línea desde el último vértice trazado hasta el primero. Tampoco debemos olvidar que, cuando N + 1 sea igual a PASO, debemos usar 0, y que, cuando N + PASO + 1 sea igual a PASO * 2, debemos usar PASO.
Para generar un cilindro, debemos usar un número elevado de caras, de modo que las bases se parezcan a un círculo.
Seguramente, a alguien se le habrá ocurrido que si hace 0 el radio de una de las bases, podría obtener pirámides o conos; sin embargo, el método no es totalmente factible debido a la rutina de eliminación de superficies ocultas. Esto es porque en la base de radio 0 no hay un solo punto, sino tantos como lados se escogieron para el prisma, por lo que, si la rutina de eliminación usa el segmento que une dos de esos vértices, como coinciden en las mismas coordenadas, el vector resultante será el cero, y siempre pintará la cara, aunque no se vea, pues el producto vectorial de cualquier vector por el vector cero da cero. Por eso haremos una rutina específica para la pirámide /cono.
Para ilustrar mejor esto, he escrito el programa PRG11.BAS, que permite rotar un prisma con eliminación de partes ocultas por el algoritmo del vector normal al plano, y el programa PRG12.BAS, que realiza el sombreado de un prisma en función de la iluminación que recibe. Los controles son los mismos que hasta ahora. Además, he aislado la subrutina que genera el prisma en el programa CILINDRO.BAS.
2: La pirámide/cono
Al igual que en el caso del cilindro, vamos a usar una aproximación. Vamos a suponer que el cono es realmente una pirámide con una base de muchos lados. Para realizarla, necesitaremos 3 datos: altura, radio de la base, y número de caras de ésta.
Vamos a calcular las coordenadas. La primera (la número cero) será la X = 0, Z = 0, Y = -ALTURA/2. Este será el vértice de la pirámide. Para hallar las coordenadas de los puntos de la base, se seguirá el mismo método que en la base inferior del cilindro.
Para crear la base, haremos un bucle N que vaya desde 1 hasta PASO - 1, y uniremos el punto N con el N + 1.
Para crear cada uno de los lados, haremos un bucle N que vaya desde 1 hasta PASO. Entonces, cada cara estará formada por la unión de:
- vértice 0 a vértice N
- vértice N a vértice N + 1
No hace falta hacer vértice N + 1 a vértice 0, pues la rutina cierra automáticamente cada cara. Tampoco debemos olvidar que si N es PASO, N + 1 debe ser 1.
Para ejemplificar lo dicho, he escrito el programa PRG13.BAS, que permite rotar un cono con eliminación de superficies por el método del vector normal al plano. También he aislado la rutina que genera el cono en el programa CONO.BAS.
3: La esfera
La esfera es, sin lugar a dudas, la más espectacular de las superficies de revolución. Vamos a ver como generarla.
Para generar la esfera, vamos a usar el método del cinturón. Se basa en coger un número determinado de cinturones o cortes de la esfera, y suponerlos, en vez de círculos, polígonos de elevado número de lados. Para entenderlo mejor sería conveniente que vieses el programa PRG11.BAS, en el que aparece una esfera en representación alámbrica y con eliminación de superficies ocultas.
La esfera quedará definida por dos conos en sus extremos superior e inferior, y un elevado número de prismas de bases diferentes entre sus extremos. La razón de usar conos en vez de prismas con una de las bases de radio cero es el evitar problemas con la rutina de eliminación de superficies ocultas.
Para generar la esfera, usaremos PASO / 2 cinturones, divididos en PASO partes. Veamos primero como calcular los vértices:
Como datos, necesitamos: RADIO, el radio de la esfera; y PASO, el número de caras en que dividiremos cada cinturón. Denominaremos PASO2 a la cantidad 360 / PASO.
El número total de vértices viene dado por la ecuación:
2 + PASO * ((PASO / 2) - 1)
Lo primero que debemos hacer es almacenar los vértices superior e inferior de la esfera. Estos serán los puntos 0 y 1, y sus coordenadas serán X=0, Z=0 para ambos, Y=RADIO para el primero e Y = - RADIO para el segundo.
Inicializamos el contador CUENTA a 2, pues los puntos 0 y 1 ya están calculados.
A continuación procedemos a calcular cada uno de los cinturones de puntos de la esfera. Para ello, hacemos un bucle F que vaya desde PASO2 hasta 180 - (PASO2 / 2), con un incremento de PASO2. Este bucle nos da la altura de cada cinturón. La razón de restar PASO2 / 2 en vez de PASO2 es la misma que en el caso del cilindro.
Llamaremos GRADO2 al valor de F convertido en radianes, RADIO2 a RADIO * SIN(GRADO2) y ALT2 a RADIO * COS(GRADO2).
Hacemos un segundo bucle, N, que vaya desde 0 hasta 360 - (PASO2 / 2), con un incremento de PASO2. Este bucle nos da el ángulo de cada punto del cinturón.
Llamamos GRADO al valor de N traducido a radianes.
Ahora, el vértice número CUENTA tendrá como coordenadas: X = RADIO2 * SIN(GRADO), Y = ALT2 y Z = RADIO2 * COS(GRADO).
Incrementamos CUENTA y cerramos los dos bucles.
También podemos asignar radios distintos para cada uno de los ejes, de modo que podemos conseguir elipsoides (por ejemplo, un balón de rugbi). En el programa generador de la esfera así lo hago.
A continuación calculamos la unión de los vértices para formar las caras de la esfera.
El número total de caras viene dado por la ecuación:
PASO * INT (PASO / 2)
La variable CUENTA indica el número asignado a cada cara.
Calculamos primero los lados de la base inferior como si de una pirámide se tratase. Para ello, hacemos un bucle N desde 0 hasta PASO - 1, asignamos 3 segmento a cada cara y unimos los vértices siguientes en este orden, tomando SIG = N + 1 (si N = PASO - 1, SIG = 0). CUENTA se inicializa a 0 y se incrementa en cada paso del bucle:
- vértice 0 a vértice SIG + 2 (pues el vértice 0 es el punto inferior de la esfera)
- vértice SIG + 2 a vértice N + 2
La razón de sumar dos a N y a SIG es que los vértices 0 y 1 son los de los extremos de la esfera, y los del primer cinturón empiezan en el 2.
A continuación calculamos las caras de la parte intermedia de la esfera. Estas son trapecios que unen dos puntos consecutivos de un paralelo con los dos puntos correspondientes del paralelo superior.
Hacemos un bucle F desde 0 hasta (INT (PASO /2)) - 3, y otro N desde 0 hasta PASO - 1. Tomamos SIG = N + 1, y si N = PASO - 1, SIG = 0. Por último, CUENTA = N + PASO + F * PASO + 2.
Asignamos a la cara número CUENTA cuatro lados, y unimos los siguientes vértices:
- vértice SIG + F * PASO + 2 a SIG + PASO + F * PASO + 2
- vértice SIG + PASO + F * PASO + 2 a N + PASO + F * PASO + 2
- vértice N + PASO + F * PASO + 2 a N + F * PASO + 2
Y cerramos los dos bucles.
Por último, calculamos la base superior. Lo haremos de manera similar a la base inferior:
Sea F = PASO * ((INT(PASO / 2)) - 2) y CUENTA = CUENTA + 1 (aprovechamos el valor del paso anterior). Hacemos un bucle N desde 0 hasta PASO - 1, hacemos SIG = N + 1, si N = PASO - 1, SIG = 0, y unimos los siguientes vértices, asignando a cada cara 3 lados:
- vértice 1 a vértice N + 2 + F
- vértice N + 2 + F a vértice SIG + 2 + F
Incrementamos CUENTA y cerramos el bucle. Con esto hemos terminado la esfera.
La rutina que genera la esfera la he aislado en ESFERA.BAS. Además, está el programa PRG12.BAS, que permite rotar una esfera sólida en tres dimensiones y eliminar las superficies ocultas, y el programa PRG15.BAS, que permite rotar la misma esfera y rellenarla con tramas en función de la luz que recibe desde un foco. En estos programas uso un paso de 15, pero se puede aumentar para conseguir mayor fidelidad. En cualquier caso, no debe ser mayor de 40, pues al ordenador no le llegaría la memoria.
4: Otras superficies de revolución
Está claro que en la vida real existen multitud de figuras que provienen de la rotación de un plano, pero que tienen formas más aleatorias y complejas. Por poner un ejemplo, supongamos una simple copa. Vemos que podríamos definirla con una serie de cortes perpendiculares al eje vertical, los cuales darían lugar a círculos de diferentes diámetros y alturas. De este modo, podemos hacer una rutina que nos cree superficies de revolución basadas en este tipo de cortes. Para ello, bastará con darle el número de cortes, y luego la altura de cada uno y su radio. De este modo, el programa lo que hará será unir el primer círculo con el segundo, éste con el tercero, éste con el cuarto, y así sucesivamente. Veamos la mecánica igual que hicimos con las otras figuras:
Lo primero que necesitamos es el número de cortes o discos en que se ha dividido la figura. Será NDISCOS. El número total de vértices de la figura será TOTV = NDISCOS * PASO, siendo PASO el número de lados de cada corte, y PASO2 = 360 / PASO. Hacemos CUENTA igual a cero.
Hacemos un bucle F desde cero hasta NDISCOS - 1, leemos de las DATAs el radio (RADIO) y la altura (ALT) del corte actual y hacemos otro bucle N desde cero hasta 360 - (PASO2 / 2) con un incremento de PASO2.
Llamaremos GRADO al valor de N en radianes. Ahora, el vértice número CUENTA tiene como coordenadas:
- X = RADIO * SIN(GRADO)
- Y = ALT
- Z = RADIO * COS(GRADO)
Incrementamos CUENTA y cerramos los bucles.
Ahora vamos a hallar las caras. El total de ellas será
(NDISCOS - 1) * PASO
Hacemos un bucle F desde cero hasta NDISCOS - 2, y un bucle N desde cero hasta PASO - 1. SIG será igual a N + 1, salvo que N = PASO, en cuyo caso será SIG = 0. CUENTA será igual a N + F * PASO.
El número asignado a la cara será CUENTA. El número de lados de la cara será cuatro, y uniremos los siguientes vértices en este orden:
- Vértice N + F * PASO a vértice N + PASO + F * PASO
- Vértice N + PASO + F * PASO a vértice SIG + PASO + F * PASO
- Vértice SIG + PASO + F * PASO a vértice SIG + F * PASO
Cerramos los dos bucles. La figura estará definida.
Un detalle muy importante: como ya explique, el radio de los cortes no debe ser nunca cero, pues daría problemas al hallar el vector normal a la superficie. Si, para hacer una parte, no queda más remedio, hay dos soluciones:
- Modificar la rutina para que todo corte de radio cero lo sustituya por un punto, y una todo como si fuesen conos en vez de prismas.
- Colocar un radio muy pequeño, p.e. 0.1 (una décima) en vez de cero.
Para ejemplificar esto, he escrito el programa PRG16.BAS. En él podremos rotar una copa definida mediante este sistema y sombrearla según una fuente de luz. Además de ésto, he aislado la rutina en REVOLU.BAS. Los usuarios de ordenadores SINCLAIR SPECTRUM es posible que reconozcan la figura, pues es idéntica a la que traía como ejemplo el programa de diseño VU-3D de la casa PSION.
Es obvio que este sistema admite más mejoras. Yo le he hecho tres: poder cerrar la figura por arriba y/o por abajo (el sistema anterior las dejaba huecas y sin cerrar), poder elegir no solo la coordenada Y del centro, sino la X y la Z también, y, por último, poder seleccionar radios distintos para cada uno de los ejes X y Z, de modo que pueda conseguir no solo círculos, sino también elipses.
Estas mejoras se pueden ver en el programa PRG17.BAS, en el que he dibujado una jarra (aunque lo cierto es que en pantalla parece un silenciador de coche 8-D). En él, además de rotarla, podrás sombrearla. Como de costumbre, la rutina aparece aislada en el fichero REVOLU2.BAS.
Como eliminar el parpadeo
Los programas de demostración que incluyo presentan un grave problema de parpadeo al animar figuras. Esto es debido a que cuando el programa tiene que pintar una nueva imagen, borra la anterior primero, y traza la nueva directamente sobre la pantalla. Como el rayo catódico es más rápido dibujando una pantalla que el ordenador borrando una y dibujando la nueva, se produce el indeseable parpadeo de la imagen. Para solucionarlo, se emplea un sistema denominado ESCRITURA EN PAGINA OCULTA. Se trata de pintar cada imagen en una zona de memoria separada, y una vez que está lista, se copia en la memoria de pantalla. Veámoslo con más detalle:
Supongamos que necesitamos 64K para almacenar una imagen en la tarjeta gráfica. Entonces reservamos otros 64K en la memoria principal (en algunas tarjetas, como la EGA o la VGA, se puede usar memoria del propio adaptador gráfico) como memoria intermedia. En esa memoria intermedia realizamos todos los cálculos y dibujos, y, una vez que hemos terminado, copiamos esa zona de memoria en el adaptador gráfico. Creamos la siguiente imagen en la memoria intermedia y cuando esté lista la copiamos en la memoria del adaptador. De este modo, como mientras calculamos una nueva imagen, la anterior se mantiene en pantalla, y como la copia de una zona de memoria en el adaptador es más rápida que el haz catódico, las imágenes se sucederán con una suavidad excelente, sin parpadeos. Este es el sistema usado en todos los programas profesionales, así como en juegos de ordenador, etc.
Aunque el BASIC admite esta técnica, solo se puede usar con tarjetas EGA y VGA, por lo que no la he usado en los programas.
Para terminar
A lo largo de este largo artículo hemos visto (los que hayan llegado hasta aquí ;-) como proyectar puntos, como rotarlos, como eliminar partes ocultas de objetos, etc. Por mi parte, poco más me queda por decir. Ahora es el momento de que pongas a trabajar tu imaginación y empieces a escribir programas en 3D. Pero ojo: existen multitud de algoritmos que no he explicado, más que nada porque este artículo no pretende ser más que una introducción. Por lo tanto, si de verdad te interesa el tema, te recomiendo que busques más información. Posiblemente aparezcan nuevos artículos en números sucesivos. Para empezar, de todos modos, lo dicho es más que suficiente.
Seguramente ya te habrás dado cuenta de que el BASIC no es el lenguaje ideal para hacer este tipo de programas, pues adolece de muchas limitaciones: escasa velocidad, poca memoria, tanto para programas como para variables, etc. Mi consejo es que, si todavía no sabes, aprendas C. Es un lenguaje muy potente, y fácil de usar. Con C se puede hacer prácticamente todo lo que se puede hacer con código máquina, pero mucho más cómodamente. Tiene pocas instrucciones, por lo que se memoriza pronto, y es realmente rápido.
Y ya para terminar, quiero agradecer desde aquí la inestimable ayuda de Jesús Cea Avión, editor de la revista, por explicarme el segundo algoritmo de rellenado, el cual me ha permitido mejorar en velocidad los ejemplos, y a Marcos Urbano y Marcos Camiña, por la increíble paciencia que demostraron al leerse todas las versiones del artículo y comunicarme los errores encontrados (supongo que no les apetecerá mucho leerse la versión definitiva :-)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-CompartirIgual 4.0 Internacional.

